-
[DISCLAIMER: while the information below has been culled with care, I'm a motor noob and there's a lot of room for error. Feel free to edit!]
After doing a bit of digging, these are my preliminary findings on motor design. Inspired by Rob Hart’s question during third week of class, which was something along the lines of given a power requirement (
P = IV), is there a difference between achieving said requirement with combination of a higher voltage – lower current versus lower voltage – higher current? If so, is one better than the other? as well as Paul Horowitz’s [latest motor findings] (http://fab.cba.mit.edu/classes/865.18/power/PWM_motor_control_rev5.pdf), I am eager to form a more fundamental understanding of how motors work and what makes an efficient motor.First, it might be worthwhile to define why we care. The answer is efficiency. A motor is a system that performs work (mass * acceleration * distance). To get to operating speed, motors require a large current – e.g. the lights dimming when an air conditioner gets plugged in. A spinning motor also acts as a generator that has coils turning inside magnetic fields, and a coil turning inside a magnetic field induces an electromagnetic field (aka back emf) which acts against the applied voltage that’s causing the motor to spin. Once the motor reaches operating speed, the amount of current required to maintain a given speed is generally minimal. The startup phase is thus the most relevant to this discourse.
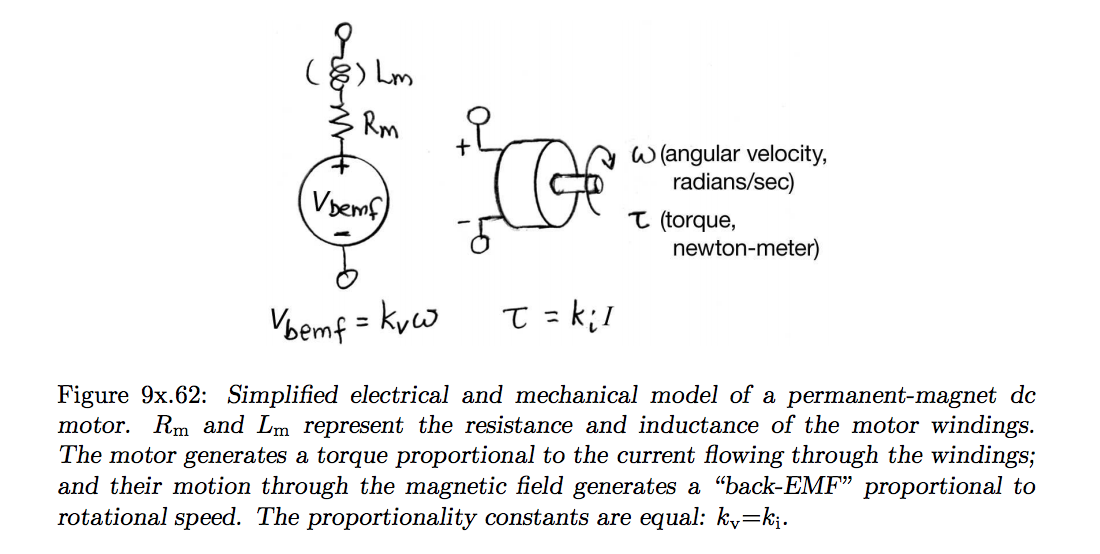
For an electric motor, efficiency is the ratio of mechanical power delivered by the motor (output) to the electrical power (input) supplied to it. I found Paul’s illustrations to be helpful in understanding the relationship between the mechanical and electrical components a motor.


Efficiency is a factor of electrical and mechanical imperfections within the motor – notably resistance losses in its windings (
I2R), friction losses, etc.At the heart of the motor is a wire coil in a magnetic field, which can be abstracted into a solenoid. ![equation for solenoid][solenoid] [solenoid]: http://www.calctool.org/CALC/phys/electromagnetism/solenoid.png Applying the formula for electromagnetic strength (
H=IN/L) means given a set of geometric constraints (space to wind wire) it is advantageous to spool as much wire as possible to achieve the greatest electromagnetic strength. This would require thinner wire and more of it, thus increasing resistance losses mentioned above. Moreover the coefficient of self-inductance for solenoid is: (L = N * (Φ/I) Since most motors are made up of several adjacent coils, it is important to consider mutual inductance. If the first coil has current running through it, a magnetic field will be produced and magnetic flux will be passed onto the adjacent coil. As such, changes in current of the first coil will change the flux of the second coil inducing and electromagnetic field in the second this relationship depends on a number of factors such as the area and the number of turns in a coil, relative orientation, the coils proximity to each other, etc. An efficient motor is one that maximizes the mutual inductance while minimizing resistance losses.….
This is about as far as I’ve gotten. Rob’s question remains unanswered, and I’m not sure whether there is an answer. Perhaps it’s just about are the motor’s wire connections, associated driver, and the ohmic losses within the system....
Whatever it is, I think it’s pretty fascinating and worthy of doing a little more digging on… Some final thoughts:
- Take a peek into trends in automotive industry and electric car design
- What role does temperature play, is there an advantage of operating a motor with different ($
I) or (V$) combinations in different climates? - These guys, [Montevideo Technology] (https://www.slmti.com), seem to have a pretty comprehensive array of products (they even offer custom windings!) – consider their white papers and/or write with a inquiry to elucidate matters further.
Please register or sign in to comment